Advanced “Either Or” Clue Solving Part 2
A lot of the Daily Challenge puzzles and Hard level puzzle packs contain games which require a more advanced knowledge of the Either Or clues.
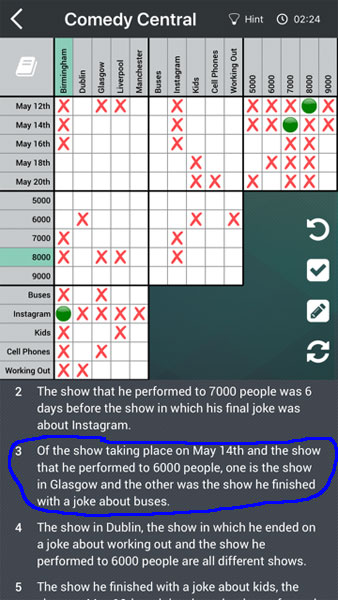
If you look at the puzzle example here, the second part of clue 3 tells us some information that might be hidden to the novice logic puzzler. From this clue, we know that Glasgow and buses are separate events but it also tells us more than this. If you look down the column on the grid you can see the player has already marked Glasgow and Buses as False . . . BUT . . if you carry on down that same column you can see that Glasgow also isn’t equal to Instagram or Cell Phones.
So, looking at the first part of the clue we know that May 14th must be equal to Glasgow or Buses; and we now know that Glasgow isn’t equal to Instagram or Cell Phones and buses isn’t equal to Instagram or Cell Phones as they are in the same section . . it therefore follows that May 14th CANNOT be equal to Instagram or Cell Phones. From a previous clue May 14th and Instagram is already filled in as false but we can now fill in May 14th and Cell Phones as false.
The same process now applies to 6000 (the other item in the first part of clue 3) which also CANNOT equal Instagram or Cell Phones so you can now fill these two boxes as false.
The same process can also be used across the rows as well as the down columns. So where we see Buses and Glasgow is already false, we can also see that Buses are not equal to Birmingham either. So that then tells us that May 14th and 6000 CANNOT equal Birmingham either.
Use this technique every time you see a clue beginning with “Of . . . .” and you’ll be able to solve some of the more difficult puzzles.